The volatility risk premium refers to the compensation that investors require for holding risky assets, such as stocks or options, that are subject to sudden price changes or fluctuations in value. However, the volatility risk premium suggests that investors can be compensated for taking on this risk. There are several reasons why the volatility risk premium exists. One is that investors are risk averse and require compensation for taking on additional risk. The volatility risk premium can be observed in the options market, where the implied volatility of an option can be different from the actual volatility of the underlying asset. If the implied volatility is significantly different from the actual one, this suggests that investors are willing to pay more for the option because they expect more volatility than what has been recorded historically.
Implied volatility vs Actual volatility
The generally acknowledged method for option pricing is using Black-Scholes-Merton model, however the quoted prices we can find on the market are slightly different from the one we would obtain just by substituting the different values: this happens because individuals wanting to sell options have some expectations on the market and are generally risk-averse, so the risk-factor, which is the volatility, will be slightly higher than the actual one. This happens also because returns are not homoscedastic, so their volatility varies over different periods and people try to guess what will happen.
To compute the implied volatility in an option price we can just solve the BSM equation with as the value to find.

The implied volatility in the S&P 500 index for options that expire in 27-35 days is represented by VIX, which is considered the fear level of the market. However, with the rise of zero days options (0DTE) it is losing its importance, since short term expectations are discounted in these new derivatives.
How to profit from VRP?
The most common way to profit from Volatility Risk Premium is selling index options and hedging the position with the index itself; this could lead to major losses in case of large price jumps, as happens in financial crises. Another strategy deploys variance swaps. This financial instrument is quite different from a usual swap, since it does not require periodic cash flow exchange and pays at strike based on the difference between the realized variance and the strike level, basing on the theoretical notional. Using variance swaps has many advantages: it offers the purest exposure to VRP, since the payout formula depends directly on realized variance and it doesn’t need a capital allocation beyond the collateral, making leverage easy. However it has one main disadvantage: the quadratic form of the payoff function, that amplifies losses. The last method is also the most straightforward, which consists of shorting VIX futures. This is also the most difficult to implement due to the change in term structure in highly volatile markets.
Index options:
Back to index options we know that the performance of these options is driven by two main factors: the directional movement of the underlying asset and the VRP (Israelov and Nielsen [2014], Ge and Bouchey [2015]). In order to remove the directional component two main methods have been developed: a short straddle and a short strangle. Straddles are just a special type of strangles, since strangles consist of a put option and a call option with the same expiration date and different strike price, while strangles have the same.
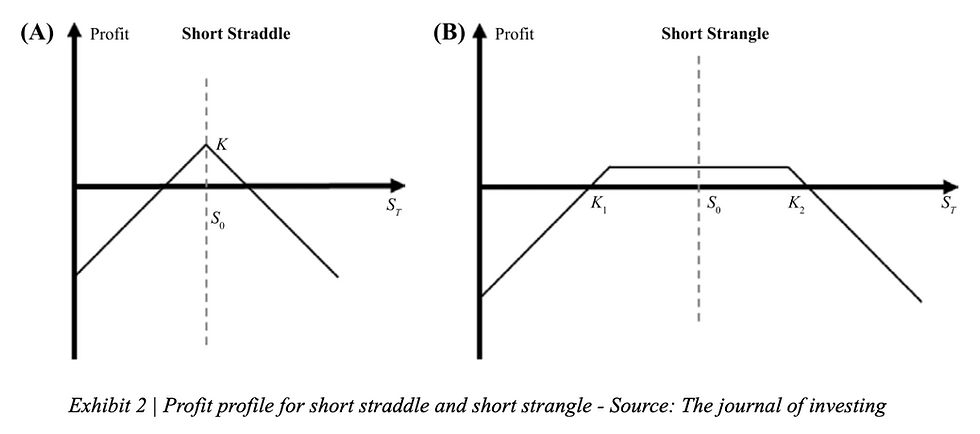
These two strategies are usually profitable if the final price of the underlying asset is close to the asset price when the contract was initiated, this happens when volatility is low. Studies show that using options to collect VRP would have been profitable in most historical periods (Bakshi and Kapadia [2003], Ge and Bouchey [2015]). One main constraint you should follow when constructing a strangle or a straddle is to try to keep a delta-neutral position. When choosing the strike prices of the options one thing that is necessary to understand is the volatility smile curve, which plots the implied volatility over the strike price and when the strike price is closer to the spot price the option tends to have a low implied volatility.

It’s crucial to understand that options with strike price really far from S tend to have low liquidity and should be not considered.
Delta Hedging:
Assuming the case where stock prices follow a Geometric Brownian Motion and no dividend are paid, so that the call option can be replicated by trading a stock and a bond we can write it as it follows:

Being not possible to hedge a position continuously, the profit from delta hedging could be different from zero. If it is hedged discreetly at intervals tn,n=0,1,...,N-1, we define t0=t and tN=t+t, so that each interval is equal to t/N. The delta hedging gains at t+ can be described by:

Research demonstrated that the distribution of discreetly hedged portfolios has a mean of zero and it is symmetric (Bertsimas, Kogan and Lo, 2000), this can also be demonstrated via simulations. After rewriting Black Scholes equation for implied volatility and substituting in the previous equation, we obtain the volatility risk premium that we can harvest.

The VRP depends on a short position of gamma, which is almost everytime positive.
Running some simulations we can show that the most profitable strategy would consist of selling options that are out of the money, but not too deeply, since this would reduce the probability of seeing the option exercised and this lowers the profit, as the table below shows.

We will not show all the computation of the VRP when considering the stock price following a Heston model because it requires advanced knowledge of mathematics, it is still possible to hedge the position with Black Scholes delta, however it is far more complicated and in this case variance swaps are the best choice.
Variance swaps:
Variance swaps are bilateral, over the counter future contracts that where at the expiry date the receiver of the floating leg pays the difference between the realized variance and the agreed upon strike. The strike K is called the fair variance and it is the one that makes the contract value equal to zero. The notional is never exchanged, since it is usually specified in terms of vega and it’s called vega notional. The payoff of a variance swap can be computed as it follows:

In this case the payoff will depend on the model chosen; the most common is the one with stochastic volatility.

However, the Heston model is not the only one we can use. Even if we assume that the stock price follows a Geometric Brownian Motion, with constant volatility, and we apply Black Scholes model for option pricing we end up with a variance swap with no value, since the implied volatility can be computed, it seems useless. Often volatility skew can be spotted, this means that the implied volatility for ATM, ITM and OTM options is different and in this case we can deploy variance swaps to capture the di↵erence between implied volatility and realized volatility. The mathematics behind the relation between a variance swap and the stock price requires the application of Ito’s Lemma. Starting from a GBM:

Applying Ito’s formula we get:

Taking integrals the total variance is:

Assuming that there are 252 business days in a year we can estimate the variance as:

The fair strike can be found in [Tsoukalas and Zeng, 2009]

Where C0 and P0 are the call option and put option prices at t = 0.
VIX index futures:
Today, VIX-based derivatives, especially futures, have surpassed variance swaps in terms of popularity. In the aftermath of the Global Financial Crisis many investors saw the need for tail-hedging via long positions in VIX futures. Several studies show that such tactics usually have negative returns, as a consequence of the contango profile (future prices are higher than spot prices) shown by the term structure of VIX. So, shorting VIX futures may be a straightforward way to harvest VRP.

In a normal volatility environment, investors should short VIX index futures with a longer tenor, in order to capture positive carry costs and roll the contracts over to generate profits. Research shows that simple futures rolling strategies can generate significant short term risk, attributable to the volatility of the short term VIX term structure. To avoid this a more sophisticated hedging strategy is needed: shorting short-term VIX futures and going long medium-term VIX futures. Other than this, another disadvantage is that the notional exposure of VIX futures is expressed in terms of vega, making it difficult to sizeVIX futures.

From this table we can see that the best strategy deploys options, they also have higher liquidity and can be easily customized. The returns of this strategy have the lowest beta exposure to the equity market and the lowest correlation with the S&P 500 index. The returns of this strategy should converge in the long term to the theoretical volatility risk premium. VIX futures need to be considered in this discussion because they have low trading costs and suffer the smallest drawdowns.
Different implementations:
Standalone VRP strategy (beta = 0)
A beta neutral short options portfolio may be an attractive standalone strategy within an overall portfolio. The strategy typically has steady, positive returns in most market environments and may be a good diversifier to equity, fixed income, and alternative allocations. While having a strong Sharpe over the long haul, the strategy can experience meaningful drawdowns during sharp market swings. Therefore allocations to it should be sized appropriately to reflect this tail risk. For those who find this strategy undesirable it can be even implemented in a multi-alternative portfolio, still with a neutral beta position.
Buy-write strategy (beta = 0.5)
This strategy type goes by various names: buy-write, putwrite, or covered call. While the specific implementation details differ among these strategies, they have similar economic exposures. The strategy’s objective is to generate equity-like returns with lower risk and beta to equity markets. Although it generally has a beta of around 0.5, it seeks to replace the lower expected returns due to a lower allocation to the equity risk premium by allocating to the VRP. Because a VRP allocation has a low correlation to equities, the strategy generally has lower volatility than a pure equity investment and thus a higher Sharpe ratio.
Volatility enhanced equity (beta = 1)
Another interesting, though less common, approach overlays a beta- neutral VRP strategy onto a beta-1 equity portfolio in order to outperform an equity benchmark. With this approach, the portfolio remains fully invested in equities and generates active risk through the VRP. The strategy seeks to outperform an equity benchmark over the long run with similar risk.


Comentários