top of page
Jul 2, 20235 min read

Vector Autoregression Models

Updated: Dec 4, 2023

Christopher Sims proposed, in 1980, the Vector Autoregression which is a multivariate linear time series model in which the endogenous variables in the system are functions of the lagged values of all endogenous variables.

That means, the basic requirements to use VAR are:

1. Two time series (variables).

2. The time series should influence each other.


Why is it called ‘Autoregressive’?

It is considered as an Autoregressive model because, each variable is modeled as a function of the past values, that is the predictors are nothing but the of the time series.

What is the difference between VAR and models like MA, AR, ARMA or ARIMA?

VAR models are suitable for analyzing multiple interrelated time series variables, while AR, MA, ARIMA, and ARMA models are primarily used for univariate time series analysis. AR models rely on past values of the same variable, MA models consider past forecast errors, ARMA models combine both autoregressive and moving average components, and ARIMA models additionally include differencing to handle non-stationarity.



What Is VAR (Vector Autoregression)


The vector autoregressive (VAR) model is a workhouse multivariate time series model that relates current observations of a variable with past observations of itself and past observations of other variables in the system. It is macroeconomic modeling without much of the a-priori expectations getting in the way. An example of this situation occurred in Australia during the global financial crisis of 2008-2009. The Australian government issued stimulus packages that included cash payments in December 2008, just in time for Christmas shopping. As a result, retailers experienced strong sales and the economy was stimulated. As a result, incomes rose.

An example suppose that we measure three different time series variables, denoted by VAR (1) is:



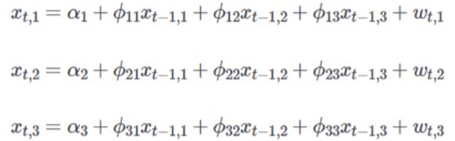
VAR models differ from univariate autoregressive models because they allow feedback to occur between the variables in the model. In this framework, all variables are treated symmetrically. They are all modeled as affecting each other in the same way. In more formal terminology, all variables are now treated as "endogenous." For example, we could use a VAR model to show how real GDP is a function of policy rate and how policy rate is, in turn, a function of real GDP.



Types of VARs


There are three types of VAR models, the reduced form, the recursive form, and the structural VAR model.

  1. The reduced form VAR model captures the dynamic relationships between variables by expressing each variable as a function of its own past values, the past values of other variables, and an error term. Ordinary least squares (OLS) regression is used to estimate each equation within the VAR system. The determination of the number of lagged values included in each equation can be done through various methods, for example a four-lag approach. It is important to note that in the reduced form VAR, the error terms will be correlated across equations when the variables are correlated.

  2. The recursive VAR approach constructs the error terms in each regression equation to be uncorrelated with the errors in the preceding equations. By including contemporaneous values as regressors, the recursive VAR establishes a causal ordering of the variables. For example, in a three-variable VAR with inflation, unemployment rate, and interest rates, the first equation has inflation as the dependent variable and lagged values of all three variables as regressors. Subsequent equations include additional contemporaneous variables as regressors. The estimation of each equation using OLS regression generates uncorrelated residuals across equations. The order of variables impacts the VAR equations, coefficients, and residuals.

  3. A structural VAR model extends the reduced form VAR model by incorporating economic theory to establish the causal relationships or contemporaneous connections between variables. The goal of a structural VAR is to uncover the underlying causal mechanisms driving the observed relationships among the variables. By incorporating economic theory, a structural VAR provides a deeper comprehension of how variables interact and influence one another within an economic framework.



How VAR is Used


Sims suggested that VARs could be of use for three purposes:

  1. forecasting economic time series

  2. designing and evaluating economic models

  3. evaluating the consequences of alternative policy actions

VARs have proven to be highly valuable, particularly in the realm of macroeconomics. They have been utilized to simulate macroeconomic shocks within the real economy and have played a significant role in policy simulations and forecasting endeavors.

Primarily, VAR stands as a sophisticated forecasting instrument, outperforming standard univariate forecasting models, particularly in discerning long-term patterns. Empirical studies on forecasting attest to the superiority of VARs over traditional univariate models and theory-based structural equation models.

In addition to their forecasting capabilities, VARs also serve as valuable tools for structural analysis. VARs allow for the exploration of responses to shocks, enabling the identification of sources of fluctuations that traditional univariate models struggle to capture. Furthermore, VARs can aid in differentiating between competing theoretical models.




Forecasting with var


To use VAR for forecasting effectively, you need to follow some steps and guidelines.

1) Identify the variables and the data sources that are relevant for your forecasting problem. Let’s take Inflation and Unemployment Rate. Reduced VAR (2) will be:




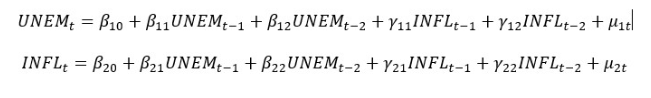
After loading the datasets of the two variables and performing data cleansing, as well as merging them, it is necessary to test for stationarity using, for example, the augmented Dickey-Fuller test.

2) Check the stationarity and the cointegration of the variables and apply appropriate transformations or differencing if needed. If the two variables are not stationary after the initial test, it is necessary to rerun the test. Stationarizing your data can provide several benefits for forecasting. Firstly, it can make the data more predictable and facilitate modeling by eliminating the influence of trends and seasonality in the data. It can also simplify the interpretation and comparison of forecasts since they are based on the original scale and level of the data.

3) Now, both the correlated features are stationary, is the moment to evaluate the performance of a model, with train test split. It involves dividing the available dataset into two separate subsets: the training set and the test set.

4) Choose the optimal lag length based on Akaike Information Criterion and Bayesian Information Criterion. Using AIC, we can use the whole dataset for training, and check among multiple models which works best. AIC is low for the best model.

5) Estimate the VAR model and evaluate its goodness of fit and diagnostic tests.

6) Generate the forecasts and compare them with the original data, the differencing operations (2) need to be reversed.


Expanding Applications of VAR Models Beyond Economics


Is VAR used only in the economic field? No, in recent years, Vector Autoregression (VAR) models have emerged as powerful tools not only in the field of economics but also in various other disciplines. While traditionally associated with macroeconomics and forecasting, VAR models have gained traction in fields such as epidemiology, medicine, and biology.

1. VAR Models in Medicine: In the realm of medicine, VAR models have proven invaluable for understanding the dynamic interplay of vital signs in cardiorespiratory patients. For instance, researchers have employed a VAR system to model the past and current relationships between heart rate, respiratory rate, blood pressure, and SpO2. By capturing the complex dependencies among these vital signs, healthcare professionals can gain deeper insights into the physiological functioning of patients and improve treatment strategies.

2. VAR Models in Epidemiology: The field of epidemiology has witnessed the growing utilization of VAR models to investigate the interactions and dynamics of infectious diseases across different age groups. By analyzing count data of past infections among various age groups, researchers can model the relationships between infection rates and identify the factors contributing to the spread of diseases like COVID-19.

3. VAR Models in Biology: In the realm of biology, VAR models have found application in modeling gene expression networks. Large networks of genes are inherently complex, with intricate relationships and regulatory mechanisms. By employing sparse structural VAR models, researchers can uncover the underlying patterns and interactions within these gene networks. This knowledge not only enhances our understanding of biological processes but also contributes to advancements in personalized medicine, genetic engineering, and disease treatment strategies.




References:





Comments

bottom of page