Introduction
Risk aversion, a fundamental concept in economics and finance, revolves around the preferences individuals exhibit when faced with uncertainty. It's a crucial aspect influencing decision-making in various domains, from investment choices to everyday life. Understanding risk aversion often involves delving into utility functions, with two commonly used models being Constant Relative Risk Aversion (CRRA) and Constant Absolute Risk Aversion (CARA). Risk aversion can be easily understood with an example: saying you were to pay $50 to play a game where you have 50% probability of winning $100 and 50% probability of losing everything, someone would take it while other would not, preferring a price slightly less than $50 to be compensated for taking the risk. Now imagine you will be forced to pay a fine which is $50 and you are given the possibility to not paying the fine or paying a $100 fine, here many more people would play the game since they are more averse to paying and their utility is higher for a certain positive result while it is higher for a uncertain negative result.
Utility functions serve as mathematical representations of an individual's preferences, showcasing how they make choices under uncertainty. These functions help economists and analysts understand how people weigh risks against potential gains or losses. In the realm of decision theory, utility functions map the relationship between the satisfaction or happiness a person derives from different outcomes and the probability associated with those outcomes. These functions essentially quantify an individual's preferences, expressing how they balance risk and reward. They must show some characteristics:
Increases one-to-one with the Mean of the outcome
Decreases as the Variance of the outcome (i.e.. Risk) increases
Decreases as our Personal Risk-Aversion increases
They are deeply related with the risk premium I would require for the uncertain result.
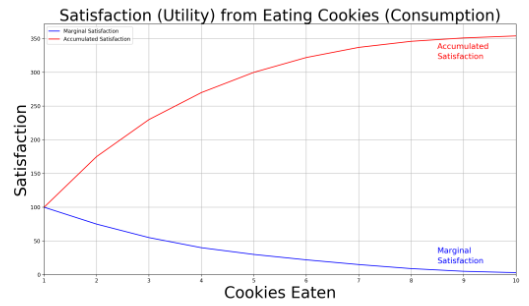
The concept of diminishing marginal utility lies at the core of these functions. It suggests that as a person's wealth or utility increases, the additional satisfaction gained from each additional unit diminishes. This principle reflects risk aversion—people generally prefer certainty over uncertainty, valuing a certain outcome more than an uncertain one with the same expected value. For example the utility function of eating cookies is concave and the concavity represents the risk aversion. For this type of functions is true that:
E(u(x))< U(E(x))
The opposite is valid for a convex function as stated by the Jensen’s Inequality
From this framework we can compute the certainty-equivalent value, which is the the amount we would pay to consume an uncertain amount and can be defined as:
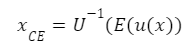
And this could be included in the computation of the absolute and relative risk premium:

CARA: Examining Absolute Risk Aversion
Contrarily, the Constant Absolute Risk Aversion (CARA) utility function assumes risk aversion remains constant in absolute terms rather than relative to wealth.
In the CARA framework, the absolute amount of risk a person is willing to bear remains constant regardless of wealth. This suggests that individuals with CARA preferences are highly sensitive to changes in wealth, exhibiting more caution and aversion to risk even as their wealth increases.
To show the mathematics behind it we take the previous equations and use x for E(x) and we develop with the Taylor expansion:
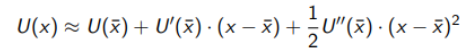
If we do the same thing around xCE we get:
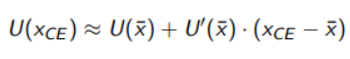
Now we take the expectation of U(x)
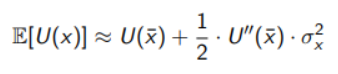
And this two equations should be equal so we get

Now substituting in the absolute risk aversion equation
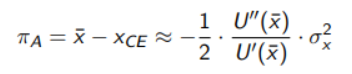
And here U''(x)/U(x) can be rewritten as A(x) or a and is the absolute risk aversion function, or a is called Coefficient of Constant Absolute Risk-Aversion.
The utility function of this model is:
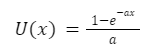
And if a=0 we have a risk neutral model with U(x) = x.
To understand how it can be applied in risk management we must refer to random variables, in particular if a variable is normally distributed the utility function will be:
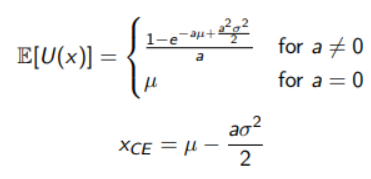
xCE in this case is the parameter that we want to maximize.
To make it clear we are going to make an example: assuming an investment of $1 that can be done on a risky asset with weight and on a riskless asset with weight 1- we want to maximize the wealth of a portfolio. If
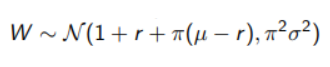
So the function we will need to maximize will be
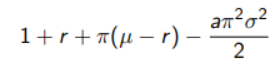
With the optimal allocation equal to
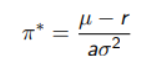
CARA: Examining Relative Risk Aversion
The Constant Relative Risk Aversion (CRRA) utility function encapsulates the idea that the degree of risk aversion remains constant relative to wealth or utility levels. Mathematically, it's expressed as, where x represents wealth or an outcome, and γ is the coefficient measuring the individual's risk aversion.
CRRA models are prevalent in economics and finance due to their simplicity and ability to capture risk preferences across various wealth levels. A higher γ implies higher risk aversion. For instance, individuals with higher γ values are more averse to risk and are willing to sacrifice potential gains for increased certainty.
Starting from the last equations from the previous paragraph we substitute in the relative risk aversion analyzed in the beginning and we get:
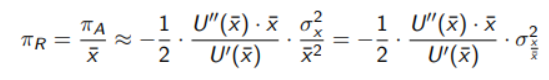
And here -(U''(x)*x)/U(x) can be rewritten as R(x) or and is the relative risk aversion function
The utility function of this model can be written as:
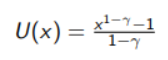
For gamma=1, U(x) = log(x). Assuming a lognormal outcome x, which will be useful in dealing with uncertainty in finance, we can rewrite it as:
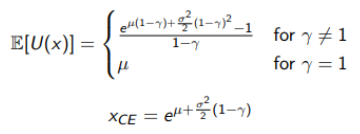
In optimization problem the function to maximize will be
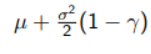
Portfolio applications
Understanding these utility functions aids in various real-world applications, particularly in finance. Investment decisions, portfolio management, insurance pricing, and public policy formulation all benefit from analyzing risk aversion. Financial institutions leverage risk preferences to tailor products that align with customers' risk profiles.
Furthermore, policymakers consider risk aversion when designing social security programs or healthcare policies, ensuring they meet the risk tolerance of the population they serve.
To apply CRRA utility to portfolio theory we must refer to Merton’s work. We choose a risky asset that follows a Geometric Brownian Motion and we assume the portfolio to be continuously rebalanced based on our data. So we first find the process for wealth (W) which is:
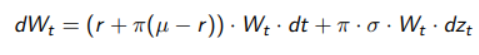
And for Ito’s Lemma we get
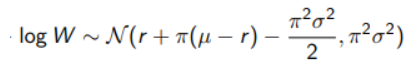
The function that we’ll need to maximize will be
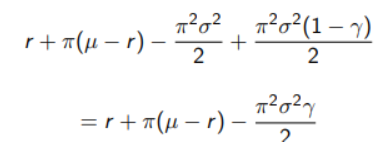
And the optimal weight for the risky asset is
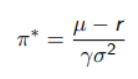
On the basis of what we have just said we can easily implement a strategy to account for the risk aversion of the investor. All we need to do is run an iterative algorithm which tries progressively different weights in the portfolio and then given the negative of the utility (in order to reduce the problem to a minimization) we can find the weight that maximizes the utility. By iterating this process with different gamma values we can easily see how risk aversion will have a negative effect on the expected returns, needless to say that volatility will be much lower. To do so we can use the Sequential Least Squares Programming (SLSQP) algorithm, which is an iterative optimization method used for solving constrained nonlinear optimization problems. It is specifically designed for problems where the objective function and constraints are smooth (i.e., they have continuous first and second derivatives).
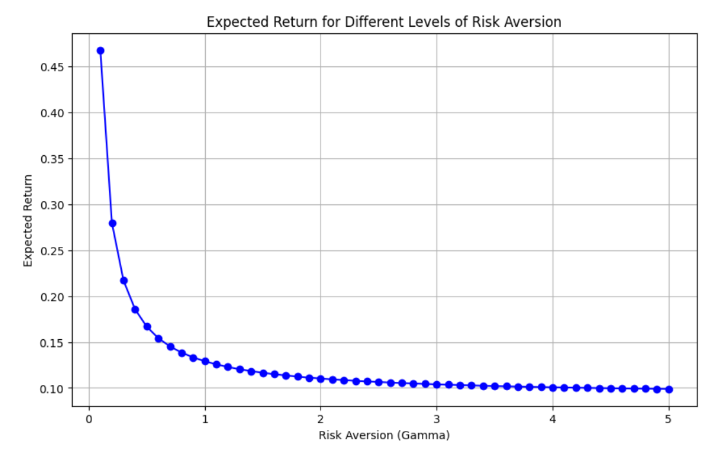
Conclusion
The comprehension of risk aversion through utility functions like CRRA and CARA provides a nuanced understanding of human decision-making under uncertainty. These models offer valuable insights into how individuals assess and weigh risks, influencing a broad spectrum of economic and financial decisions.
By integrating these concepts into economic theories and practical applications, economists, policymakers, and financial professionals can better navigate the complexities of risk and uncertainty, ultimately enhancing decision-making processes for a more efficient and stable economic environment.


Comments