INTRODUCTION
What is the Sharpe ratio
For individuals first approaching the financial world, one of the first concepts encountered is the Sharpe ratio. Due to the fact that such an index is quite easy to understand since it is founded on simple notions and it involves really common statistical principles. It can be defined as a measure of “risk-adjusted return”, developed by Willian F. Sharpe, who won the Nobel Prize in Economics for his works on the Capital Asset Pricing Model, in 1966. It is calculated as it follows:

It represents the excess return in relation to the risk, which is expressed by the volatility of the portfolio, calculated as the standard deviation. The risk-free rate is usually represented by a short term government bond, which theoretically should be free of default risk, however this could be easily substituted by the €STR (euro short term rate) which is an unsecured overnight rate for banks to borrow in euro, we will not go further in this topic. A negative ratio means that the risk taken was too high and the returns were lower than what they could have been without taking any risk. Being merely a ratio it is commonly used to compare different portfolios in order to see their different risk-adjusted returns, but it cannot give us any further information.
Someone could suggest that the formula for the Sharpe ratio is in a way similar to the one for the t-test in statistics where:

This could be translated into a test for the significance of returns higher than the average of the population, which could be identified with the risk-free return. A higher Sharpe ratio would mean a higher probability of the portfolio’s returns exceeding the risk-free rate.
Assumptions
On account of the fact that we use the standard deviation to calculate this ratio, we take for granted that such a statistic is an effective measure of the portfolio risks. This implies also that the returns are normally distributed. The second hypothesis we should make refers to the efficient frontier hypothesis. This was introduced by Harry Markowitz in 1952 and it is a derivation of the Modern Portfolio Theory (MPT), which is a well-known theory that states that investors choose a portfolio in order to maximize its return given a level of risk. This theory was so important that Markowitz was awarded with the Nobel Prize. Commencing from this idea the economist theorized that an investor can construct a portfolio of different securities, which can be either characterized by low returns and low risks or by high returns and higher risks, in order to increase its returns without increasing the risks, by taking into account both the correlation and the variance of every security. From these assumptions we know that investors choose portfolios in order to maximize the returns and minimize the risk and in this sense they are rational.

The graph above was obtained by generating 50,000 random portfolios with the returns from the last five years. Investors should only build their portfolios so that they follow the red line, which is the optimum relationship between returns and a given level of risk. No one should buy a portfolio that has the same return of another one but a higher risk.
The third assumption we are going to make is the absence of friction in the market, so that there are no costs for transactions, this assumption is supported by the development of new technology and the increase in competition between different platforms which reduces the costs drastically. In this article we will not consider the effect of taxes on capital gains.
Loss-averse investors
The Sharpe ratio poses on the same level positive returns and negative returns, without considering that most investors are risk-averse and a negative return would have a higher impact than a positive one. The assumption here is that investors are risk neutral, so they evaluate investment alternatives just for their payoffs, ignoring the potential downside risk. An example of this idea could be found in the following experiment: if you were given the opportunity to toss a coin and if you lose you pay $100, how much do you need to win to make the bet attractive? If the answer is anything above $100, this is loss-aversion. This theory belongs to behavioral finance and finds its roots in the work of Daniel Kahneman and Amos Tversky, two psychologists that developed the prospect theory.

The X-axis measures the value of a gain or of a loss, while Y-axis measures how we value that gain or loss. As the image above shows, the absolute value we give to a loss is higher than the one of a gain of the same magnitude. Loss aversion ìs extremely complex and depends even on the set point we want to keep as reference (status quo), this translates in a more risk-seeking behavior over losses and a more risk averse over gains. When operating on financial markets there could be some differences in investors’ perception between a bull market and a bear market.
Slightly different is the idea of risk-aversion, which says that the expected payoff being equal, the investor prefers a lower level of risk. Since this should be true for every investor, they should buy portfolios that maximize the Sharpe ratio, given that this is efficient. There shouldn’t be two portfolios with the same numerator but different denominator or vice versa, since the Sharpe ratio tells us the excess returns per unit of “risk”.
Ex ante or ex post
The Sharpe ratio may be computed both:
Ex-ante, with the objective of making investment decisions based on expected returns and forecasted volatility that an individual gets from historical information of the asset taken in consideration.
Ex-post, with the main objective of evaluating performances of funds in a backward looking manner, based on observed returns and volatility of the fund taken in consideration in the time horizon selected.
The main concern with the Ex-ante Sharpe ratio is due to the uncertainties in financial markets which prevents individuals from being confident about expected returns of assets, thus making the Sharpe ratio less significant, due to the fact that such statistical index is based on expected returns and volatility. Therefore we can introduce the concept of VaR which helps us deal with unsystematic risk and possible portfolio losses and profits.
Value at risk
The notion of Value at Risk, or commonly called “VaR”, gained strong relevancy in the late 1980s (but its roots harken back to the 1920s) as the preceding decades had experienced considerable volatility in exchange rates, interest rates, and commodity prices. As a result of the previously mentioned trends, financial institutions turned to the use of complex derivative instruments to hedge their risk exposure. This led to the creation of portfolios composed of these sophisticated financial instruments, which were often traded frequently and difficult to evaluate in terms of risk. The frequent changes in the magnitudes of these risks made it challenging to quantify the overall market risk of a portfolio. Thus, there was a growing demand for a clear and quantitative measure of market risk at the portfolio level.
Hence VaR may be defined as a single, summary statistical measure of possible portfolio losses, therefore it is a proxy to describe the magnitude of likely losses in a portfolio. VaR is a measure of losses resulting from "normal" market movements. Losses greater than the VaR are suffered only with a specified small probability. Generally speaking, having established a confidence level, we can define the Value at Risk as 100% - Confidence Level. If you deem a loss that is suffered less than 5 percent of the time to be a loss resulting from unusual or "abnormal" market movements, then a threshold divides the losses between those from "normal" market movements and those from abnormal movements. Using this 5 percent probability as the cutoff means that such an identified threshold is the approximate VaR. The probability used as the cutoff doesn't need to be 5 percent, it can actually be established by the users.
When estimating VaR, three main variables are required:
The confidence level, which could be 99%, 95%, 90% and so on. Such variables allow us to check the reliability of VaR as an explanatory variable.
Target horizon t.
Estimation model, meaning whether to choose the lower or upper tail of the empirical distribution.

The three basic approaches to estimate VaR are:
Historical simulation: The method in question relies on certain assumptions, primarily regarding the statistical distributions of market factors. It involves analyzing historical market rate and price changes to construct a distribution of potential future profits and losses for a given portfolio. The VaR, or the amount of loss exceeded only a small percentage of the time, is then estimated based on this distribution. To build this distribution, observed changes in market factors are examined and applied to the portfolio in hypothetical scenarios. In each scenario, the portfolio's value is adjusted based on the current market prices of its underlying assets. This allows us to compute the profits and losses that would occur in each hypothetical situation based on historical rate and price changes. After determining the hypothetical mark-to-market profit or loss for each scenario, we can then establish the distribution of the portfolio's potential profits and losses, which in turn allows us to compute the VaR.
Delta-normal approach: The underlying assumption of such methodology is based on the thesis that the inherent market factors have a multivariate normal distribution, which is a type of probability distribution which is used to model a set of random variables that are correlated between each other. Under this assumption the distribution of mark-to-market portfolio profits and losses is generated, assumed to be normal as well. Having computed the distributions of portfolios, standard mathematical properties of the normal distributions (such as a value of 1.96 for 2 standard deviations, in other words 95% confidence interval or a value of 1.65 for 90% confidence interval) are used to determine the VaR, to put it differently to determine the loss that will be equaled or exceeded a percentage of times.
Monte Carlo simulation: Such technique is in many ways similar to the Historical simulation method, with the main difference that in the following technique the individual seeking to find the VaR chooses a statistical distribution that is believed to adequately capture or approximate the possible changes in the market factors, instead of executing the simulation using the observed changes in the market factors over the last periods to generate a specific amount of hypothetical portfolio profits or losses. Through a randomized generator the individual is then able to generate thousands or perhaps tens of thousands of scenarios in which the market factors shift; then based on the current portfolio and the distribution of possible portfolio profits or losses this changes are used to construct thousands of theoretical scenarios on the portfolio’s behavior and as a last step the VaR is determined from this distribution.
ALTERNATIVES
Modigliani risk-adjusted performance
Modigliani risk-adjusted performance, also known as M2 or MRAP, is used to evaluate the performance of a portfolio based on a certain benchmark. It was developed in the 1990s by Nobel laureate Franco Modigliani. It measures the excessive returns over the expected returns of a portfolio, in proportion to the risk of the portfolio. It can be defined as follows:
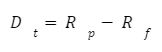
This represents the excess returns of a portfolio, since Rp is the return of the portfolio and Rf is the risk-free rate of return.
Then we have the Sharpe ratio, which can be written as

where D is the average of the excessive returns and sigmaD is the standard deviation of these returns.
Then we have:

Where S is the Sharpe ratio, sigmaB is the standard deviation of the benchmark (which usually is the market portfolio) and Rf is the average risk-free rate for the period.
If we want to substitute S we can write it as:

In the original paper Modigliani gave us even the relationship between the Alpha and this ratio, which is:

The relative riskiness is compared to the one of the market, so we can better observe how the portfolio has performed compared to the market and we can even see if the risk of the portfolio has been rewarded or it is just too high and thus is not efficient.
However, the results we obtain are no different from the one obtained with the Sharpe ratio, since it is based on the same formula. The main advantage is that the results are in percentage and are easier to interpret. It is also more versatile, since the same formula can be used with different measures of risk, such as Beta and it can be used to compare the returns to whichever portfolio we want to use as benchmark, not only the market one.
Sortino ratio
The Sortino ratio compensates for the loss-aversion of the investors and leads to different results than the Sharpe ratio. It considers only the returns that fall below the expected value or the negative returns. The formula for the Sortino ratio is the following one:

Where R is realized return of the portfolio, T is the expected rate of return for the portfolio and DR is the target semi-deviation, or downside deviation. To better understand what is meant with the standard deviation of the returns below the target we can refer to the square root of the probability-weighted squared below-target returns. This is coherent with the loss aversion of the investors, since we square the below-target returns, in formula:

Where DR is the downside deviation, T is the annual target return, r is the random variable for the annual returns distribution and f(r) is the distribution of returns, which can be for example a log-normal distribution. This formula is for a continuous variable and not a discrete one, because the discrete-time formula would identify different risk-levels and bias the results. The logic behind is that the stock's prices follow a random walk (to understand it better see Wiener process). Just to be clear this is the formula for the downside deviation in discrete time:

Where R0 is the target return and Ri is the effective return.
The problem that is being solved by this ratio is the loss-aversion of investors, it is not focused on maximizing gains but on minimizing losses.
V2 ratio
The V2 ratio is a mix of the Sharpe ratio and the Sortino ratio; its main goal is to measure the excess return per unit of exposure to loss, while taking into account the psychology of the investor, so the losses weigh more than gains. The formula for this ratio is the following:

where Vi is the ratio between the value of the investment and the value of the benchmark at time i, V0 and Vi are the initial and the final value, ViP is the peak value reached during the period and finally n is the number periods and P is the number of identical periods.
It was created in 2011 by Emmanuel Marot, who worked for a quantitative trading company. As usual the best idea is to use as benchmark an index or the market portfolio.
Application of Kelly criterion to investments
This idea is derived from probability theory, usually it is needed to determine the optimal amount to “invest” for a bet, in fact the first usage was for gambling. It is important to notice that it is calculated ex ante, based on historical data. It has seen many criticisms because it doesn’t maximize the expected value of the utility function of the results; however, if the utility function is logarithmic it is maximized.
Recent studies demonstrated that portfolios with a normal distribution of returns, optimized with the kelly criterion, had the best performance even compared with identical portfolios on the efficient frontier.
One main assumption is that the probability of the different outcomes is known. This is not the case of investments, so the optimal strategy should involve investing just a fraction of the result. We will start by explaining the basic formula for investment which is.

Where p is the probability of the positive outcome and q=1- p, and a is the fraction that is lost in the negative outcome, while b is the fraction earned in the positive outcome. If the result is negative it is better to take the opposite part in the bet and if the result is higher than 1 it is optimal to use leverage. To demonstrate the first equation we can then derive that the rate at which the capital is expected to grow, given that a positive outcome leaves us with 1+fb with probability p and a negative outcome leaves us with 1-fa with probability q:

To maximize it we need first to derive it, but it is easier if we take the logarithm

The same conclusion was the one that Bernoulli reached: the best investment alternative is the one with the highest geometric mean.
When analyzing investment opportunities the kelly fraction is calculated from existing data, such as the expected value and the volatility and in particular when studying single-assets investments we can use the geometric Brownian motion to estimate the optimal fraction to invest. Starting from the Itô’s interpretation of the Stochastic Differential Equation, which identifies the pattern followed by the stock price, which is the following:

With Wt being a Wiener process, is the drift rate and is the standard deviation, all of these are constants. And the analytic solution under Itô’s interpretation is:

We won’t show all the computation underlying this demonstration as it is beyond our objective and requires the knowledge of Itô’s calculus. This solution is a log-normally distributed random variable with:

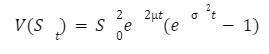
Going back to the previous equation we can take the logarithm and rewrite it as:

Now we can show how this could be applied with an example, given that we can create a portfolio with both assets (S) and bonds, and f is the fraction invested in assets and 1-f the one invested in bonds, the expected one-period return is:

However the log return G(f) is generally more used:

Notice that the value that maximizes the log return function is actually really close to the Sharpe ratio.
After all this math we will provide an example to show how it works. Given the mean return () for a stock of 15%, the risk-free rate at 5% and the volatility at 12.5%, we can calculate the optimal Kelly leverage with (0.15-0.05)/(0.125)2 which gives us a value of 6.4, this means that we should borrow 5.4 times our initial budget, this is just a theoretical example. But then we can even apply the Sharpe ratio to this result in order to get an estimation of the long-term compounded growth rate, which is:

This is the excess return we should expect from our portfolio. What the Kelly criterion says is that the leverage should be always the same, so if we have a profit we should borrow more money and invest, while if we lose we should sell to go back to the original ratio. Even if this doesn’t sound efficient for many traders it is the optimal strategy.


Σχόλια